Diffusion Models Encode the Intrinsic Dimension of Data Manifolds

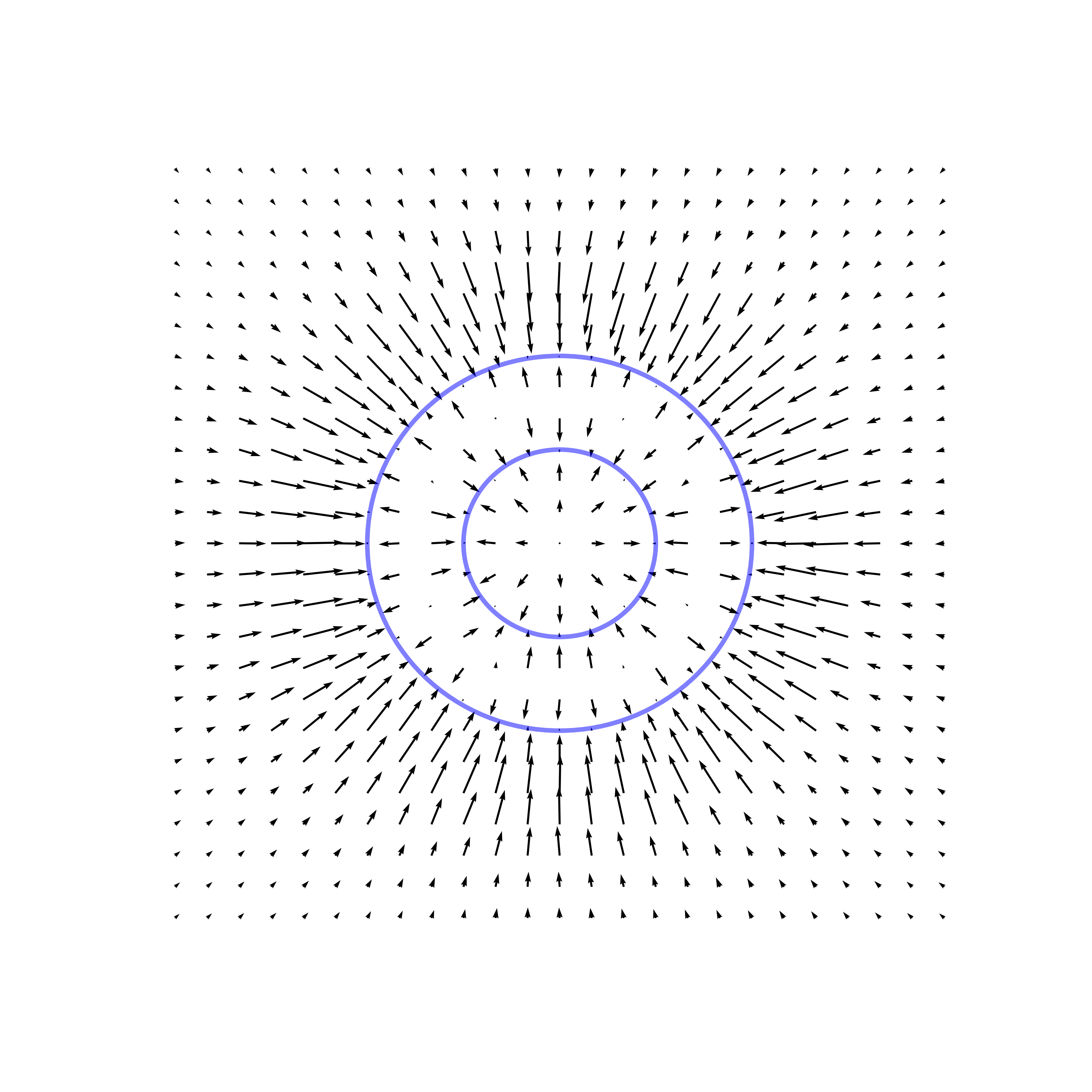
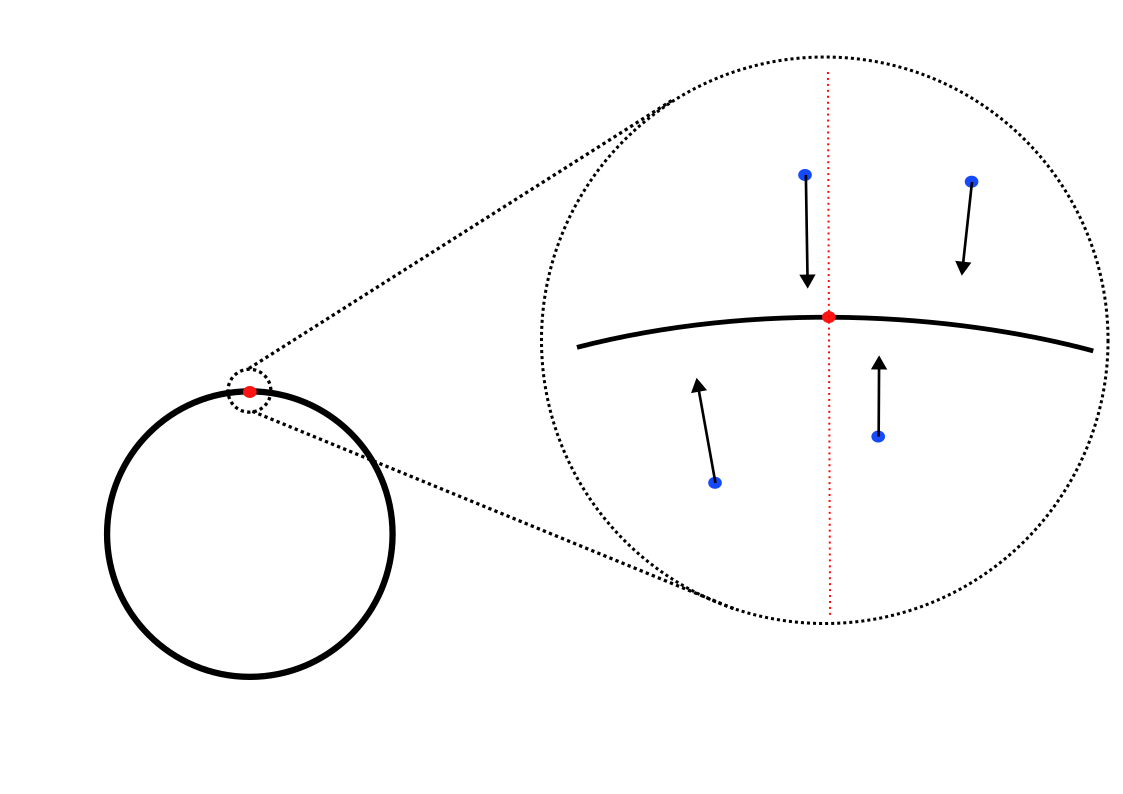
Score Field Drawing

Overview

In this work, we theoretically and experimentally prove that diffusion models, extensively used in generative modeling, capture the intrinsic dimension of the data. We introduce a novel method for estimating this intrinsic dimension directly from a trained diffusion model.

Problem Setup

We consider the following setup:

  1. There is a data manifold \( \mathcal{M} \) of intrinsic dimension \( k \), embedded in an ambient Euclidean space \( \mathbb{R}^d \), where \( d \gg k \).
  2. There is a probability distribution \( p \) that is highly concentrated around \( \mathcal{M} \).
  3. We are given a finite sample of data \( \{ x_i \}_{i=1}^n \subseteq \mathbb{R}^d \) generated from \( p \).
Diffusion models are generative models designed to learn \( p \), but they don't explicitly find \( k \). We show how one can extract \( k \) by training a diffusion model on the data.

Diffusion Models and the Score Function

We consider an Itô diffusion:

\[ dx = f(x, t)\, dt + g(t)\, dW \]

The time-reversed stochastic differential equation (SDE) is:

\[ dx = \left[ f(x, t) - g(t)^2 \nabla_x \ln p_t(x) \right] dt + g(t)\, dW \] Diffusion models \( s_\theta(x, t) \) are essentially trained to approximate the score function \( \nabla_x \ln p_t(x) \), which represents the gradient of the log-density of the noisy data distribution at time \( t \). Even if they are trained to predict the noise \(n\) or the unperturbed image \(x_0\), their output can be trivially rescaled and shifted to approximate the score function.
Forward and Reverse SDEs

Figure: Forward and reverse SDEs

Key Observation: Score Field Perpendicular to the Manifold

For small diffusion times \( \varepsilon \), the score function \( \nabla_x \ln p_{\varepsilon}(x) \) becomes approximately perpendicular to the manifold \( \mathcal{M} \).

To formalize this observation, let \( \pi(x) \) denote the projection of the point \( x \) onto \( \mathcal{M} \), \( \mathcal{N}_{\pi(x)}\mathcal{M} \) denote the normal space and \( \mathcal{T}_{\pi(x)}\mathcal{M} \) denote the tangent space of \( \mathcal{M} \) at \( \pi(x) \). The score vector \( \nabla_x \ln p_{\varepsilon}(x) \) predominantly lies within the normal space \( \mathcal{N}_{\pi(x)}\mathcal{M} \). Mathematically, this means that its projection onto the normal space is significantly larger than its projection onto the tangent space: \[ \left\| \text{Proj}_{\mathcal{N}_{\pi(x)}\mathcal{M}} \left[ \nabla_x \ln p_{\varepsilon}(x) \right] \right\| \gg \left\| \text{Proj}_{\mathcal{T}_{\pi(x)}\mathcal{M}} \left[ \nabla_x \ln p_{\varepsilon}(x) \right] \right\|. \] This phenomenon occurs because, at small \( \varepsilon \), the probability density \( p_{\varepsilon}(x) \) is sharply concentrated around \( \mathcal{M} \). The variations in \( p_{\varepsilon}(x) \) are much more pronounced in the normal direction than in the tangent direction, causing the gradient \( \nabla_x \ln p_{\varepsilon}(x) \) to point primarily towards \( \mathcal{M} \) along the normal.

Score Field Drawing

Intrinsic Dimension Estimation Method

This key observation suggests that by sampling sufficiently many perturbed points around a datapoint \( x_0 \in \mathcal{M} \), the score vectors at these points will span the normal space \( \mathcal{N}_{x_0}\mathcal{M} \). This means that if we collect the score vectors in a matrix and perform svd on this matrix, we should see a spectrum drop exactly at the dimension of the normal space \(\mathcal{N}_{x_0}\mathcal{M}\). This insight forms the basis of the following straightforward algorithm for extracting the intrinsic dimension from a trained diffusion model.
Algorithm: Intrinsic Dimension Estimation
Input:
  • \( s_\theta \): trained diffusion model (score function)
  • \( t_0 \): small sampling time
  • \( K \): number of perturbed points
Algorithm:
  1. Sample \( \mathbf{x}_0 \) from the dataset \( p_0(\mathbf{x}) \).
  2. Set \( d = \text{dim}(\mathbf{x}_0) \).
  3. Initialize an empty matrix \( S \).
  4. For \( i = 1, \dots, K \):
    • Sample \( \mathbf{x}_{t_0}^{(i)} \sim \mathcal{N}(\mathbf{x}_0, \sigma_{t_0}^2 \mathbf{I}) \).
    • Append \( s_\theta(\mathbf{x}_{t_0}^{(i)}, t_0) \) as a new column to \( S \).
  5. Perform Singular Value Decomposition (SVD) on \( S \) to obtain singular values \( (s_i)_{i=1}^d \).
  6. Estimate \( \hat{k}(\mathbf{x}_0) = d - \arg\max_{i=1,\dots,d-1} (s_i - s_{i+1}) \).
Output:
  • Estimated intrinsic dimension \( \hat{k}(\mathbf{x}_0) \).

Theoretical Results

Using the notion of tubular neighbourhood and Morse theory, we rigorously proved the following theorem, confirming our initial intuition. Full details of the proof are provided in Appendix D of the paper.

Theorem

The ratio of the projection of the score \( \nabla_{\mathbf{x}} \ln p_t(\mathbf{x}) \) onto the tangent space of the data manifold \( T_{\pi(\mathbf{x})}\mathcal{M} \) to its projection onto the normal space \( \mathcal{N}_{\pi(\mathbf{x})}\mathcal{M} \) approaches zero as \( t \) approaches zero, i.e., \[ \frac{\|\mathbf{T} \nabla_{\mathbf{x}} \ln p_t(\mathbf{x})\|}{\|\mathbf{N} \nabla_{\mathbf{x}} \ln p_t(\mathbf{x})\|} \to 0, \quad \text{as } t \to 0. \] Here, \( \mathbf{N} \) and \( \mathbf{T} \) are projection matrices onto \( \mathcal{N}_{\pi(\mathbf{x})}\mathcal{M} \) and \( T_{\pi(\mathbf{x})}\mathcal{M} \), respectively. Thus, for sufficiently small \( t \), the score \( \nabla_{\mathbf{x}} \ln p_t(\mathbf{x}) \) is (effectively) contained in the normal space \( \mathcal{N}_{\pi(\mathbf{x})}\mathcal{M} \).

Experiments

We validated our method on various datasets, both synthetic and real-world, comparing it with traditional intrinsic dimension estimation techniques.

Synthetic Manifolds

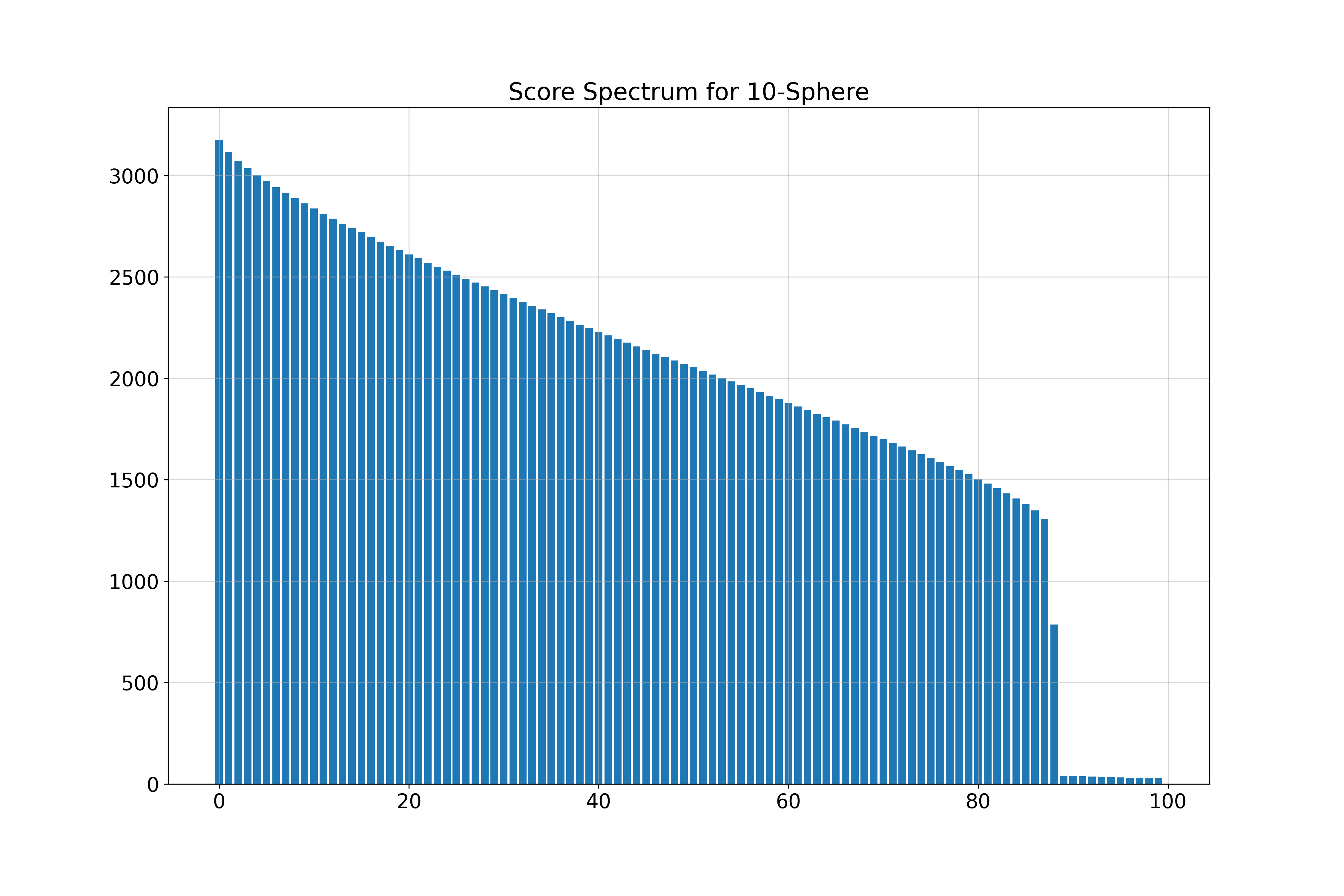
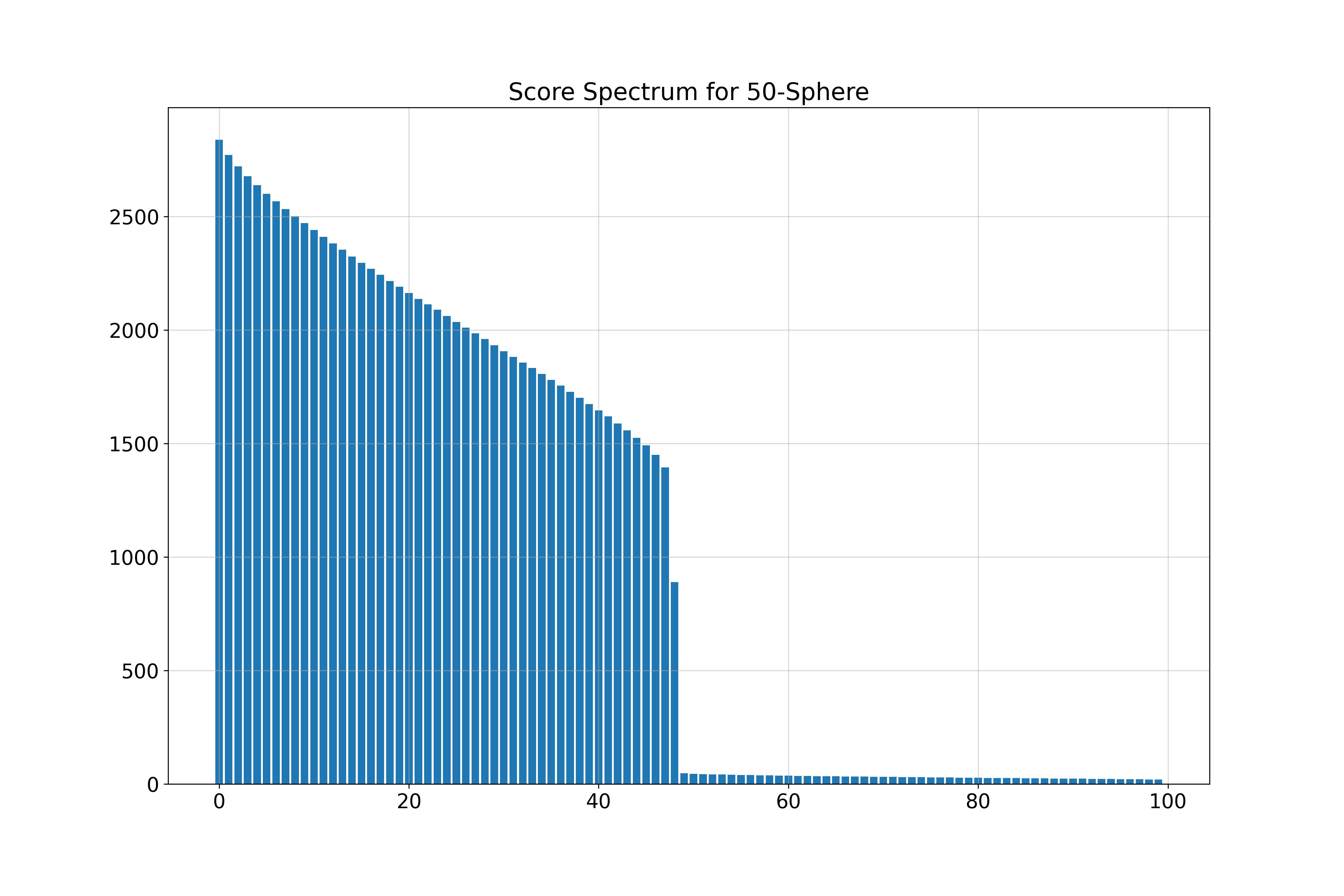
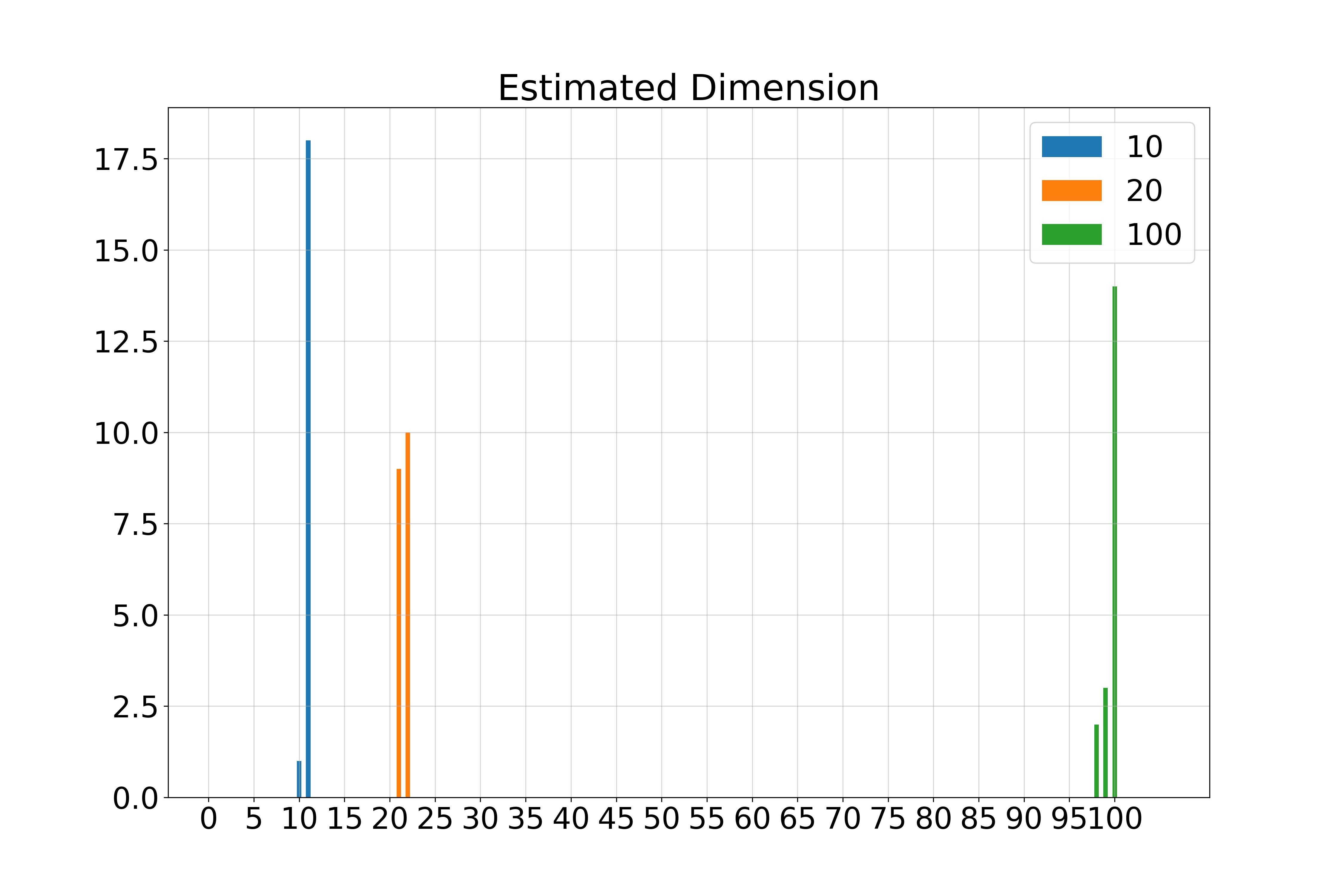
\( k \)-Spheres in 100 Dimensions

We generate \( k \)-dimensional spheres embedded in \( \mathbb{R}^{100} \) using random isometric embeddings.

  • 10-Sphere (\( k = 10 \)): Estimated \( \hat{k} = 11 \)
  • 50-Sphere (\( k = 50 \)): Estimated \( \hat{k} = 51 \)
10-Sphere 50-Sphere

Mammoth Manifold

A 2D manifold embedded in 100 dimensions. Estimated: \( \hat{k} = 2 \)
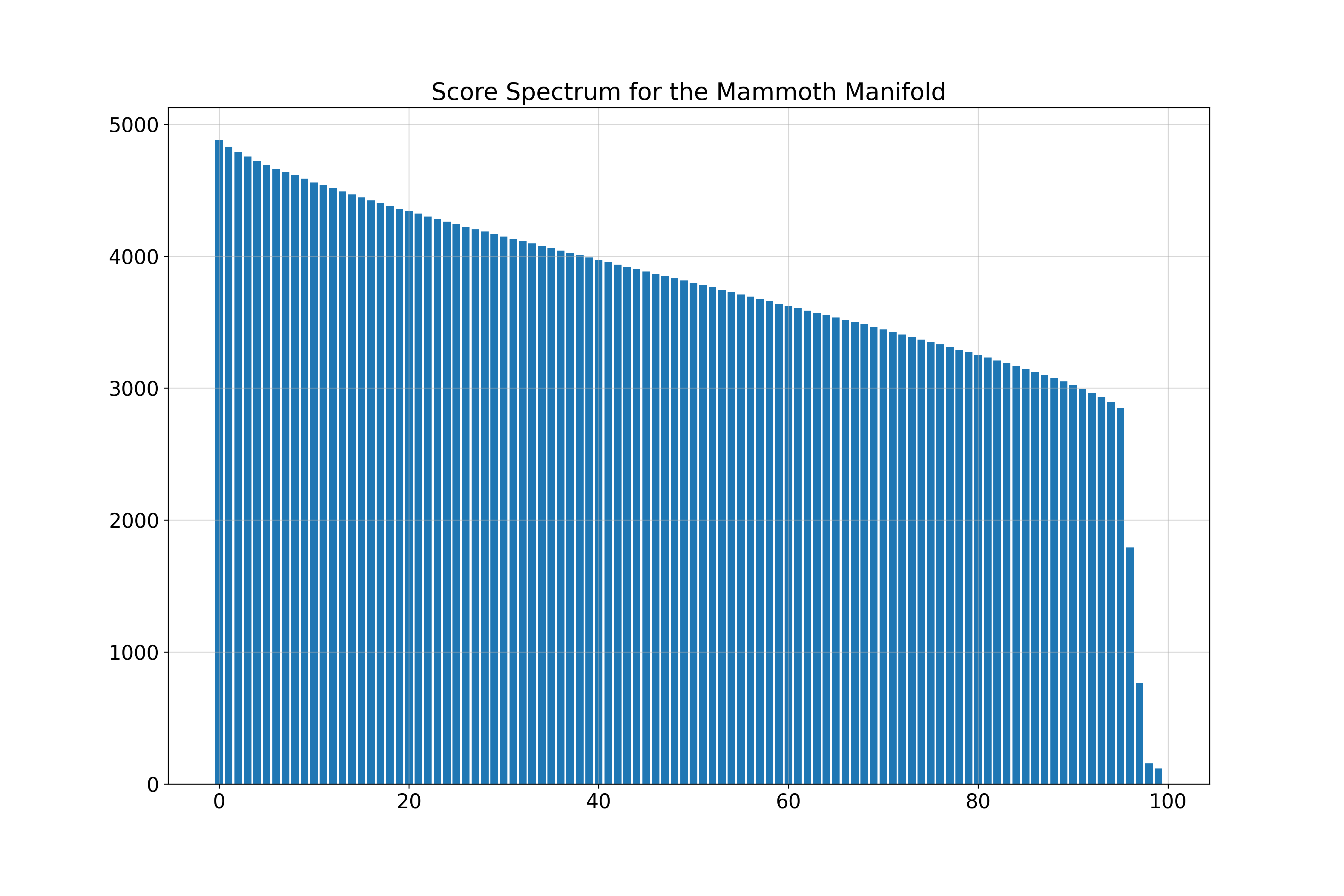
Mammoth Manifold Mammoth Spectrum

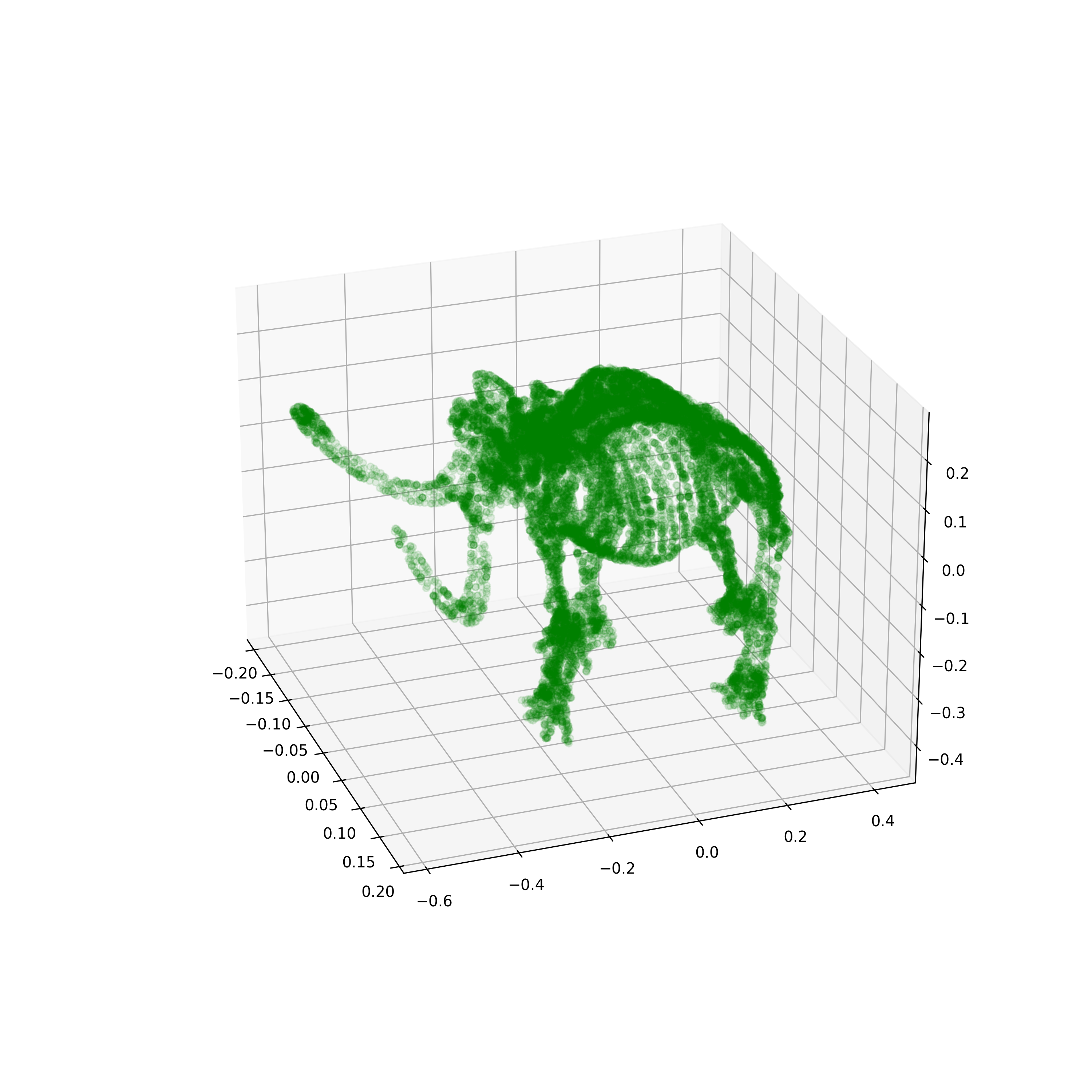
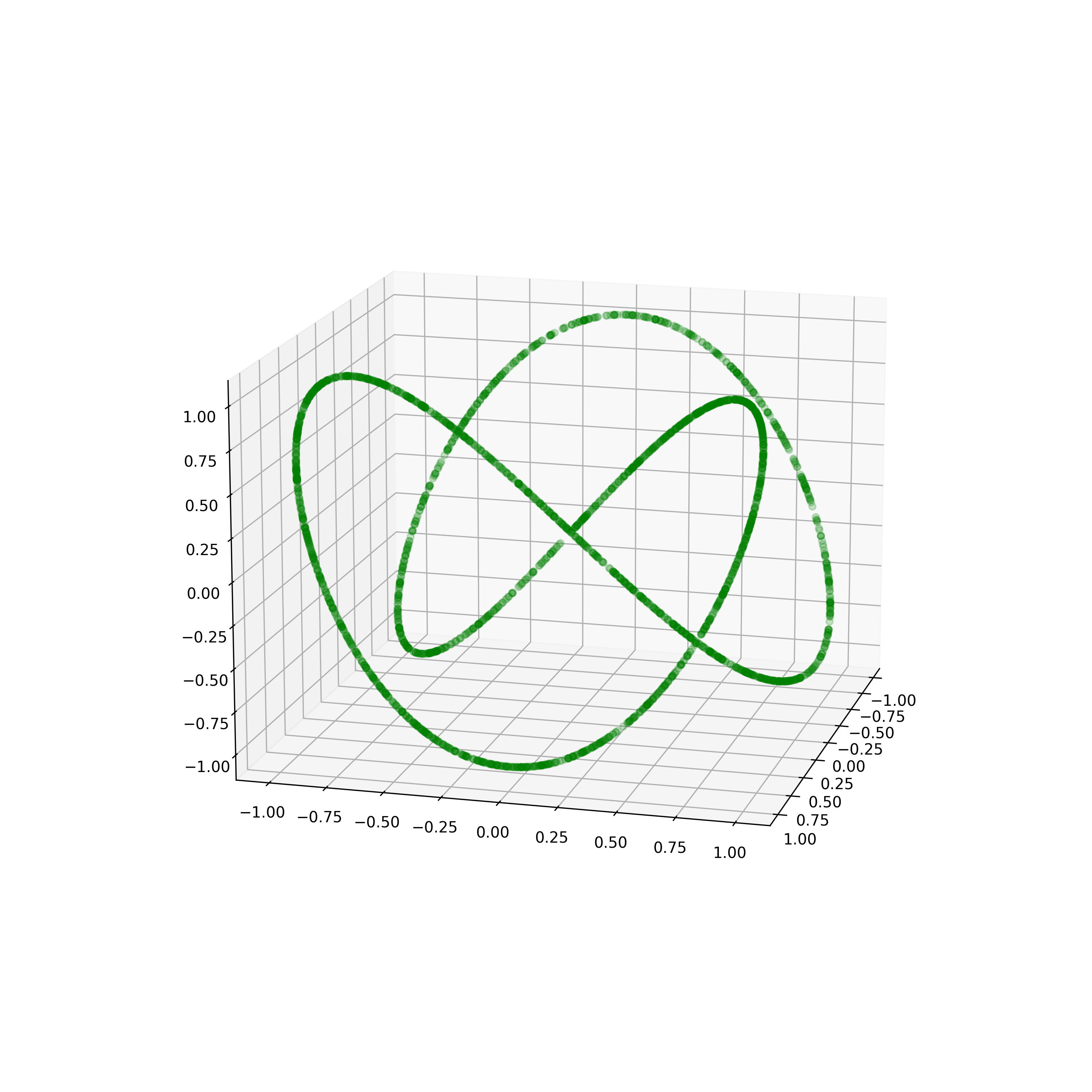
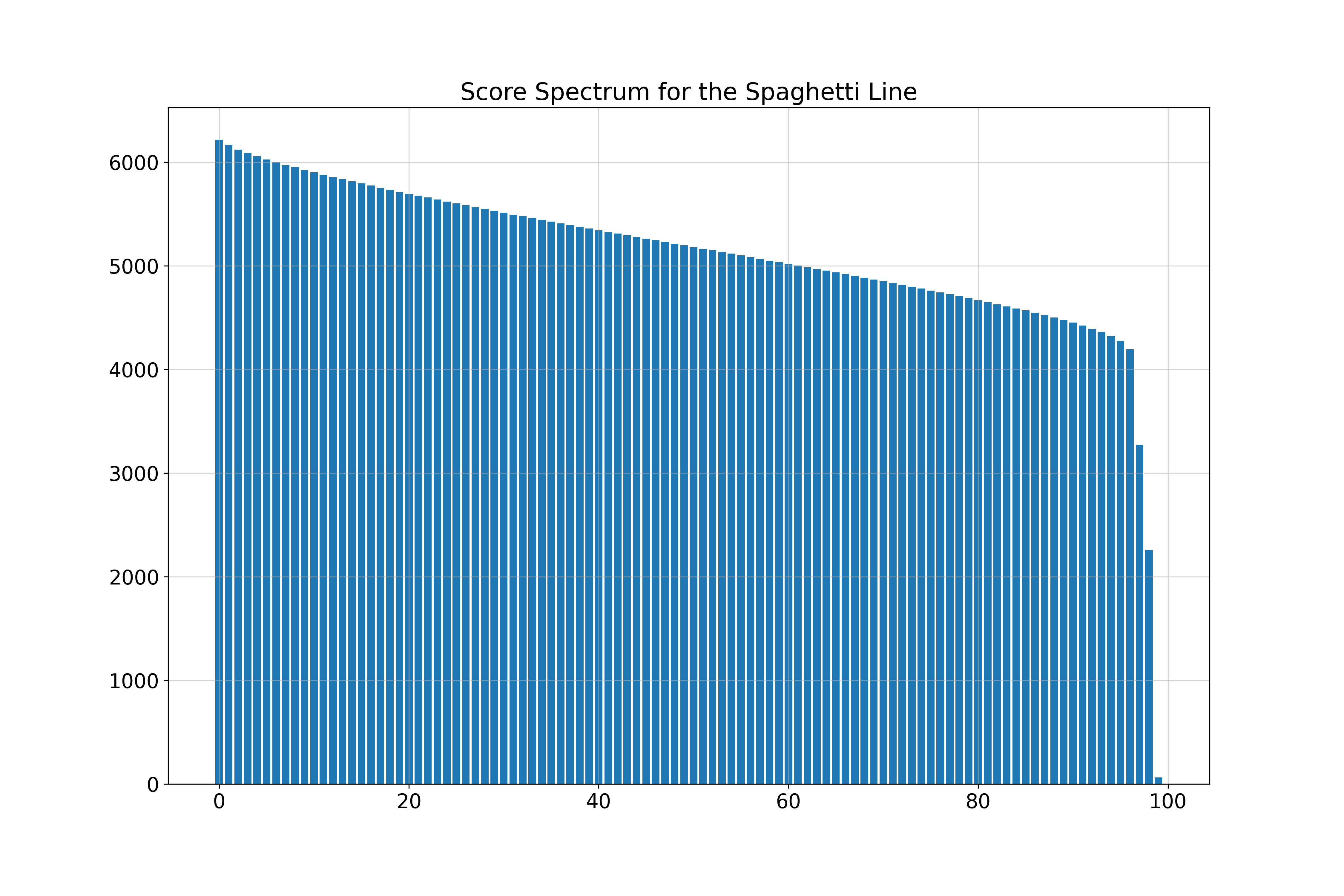
Spaghetti Line in 100 Dimensions

A 1D curve embedded in \( \mathbb{R}^{100} \). Estimated: \( \hat{k} = 1 \)
Spaghetti Line Line Spectrum

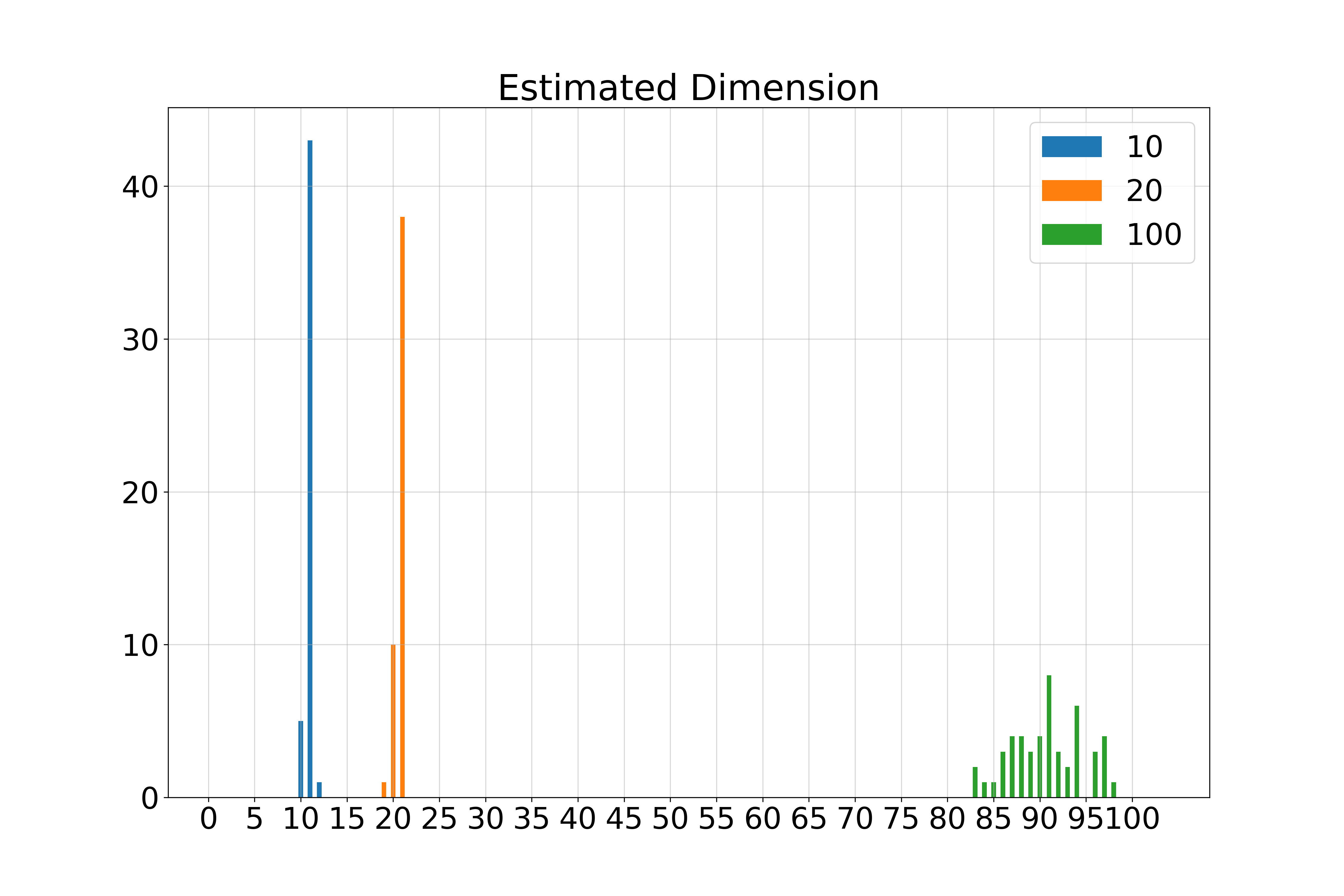
Union of Manifolds: 10-Sphere and 30-Sphere

We analyze a dataset composed of a union of two spheres.

Union Spectrum

The estimated dimensions vary locally, reflecting the manifold’s structure.

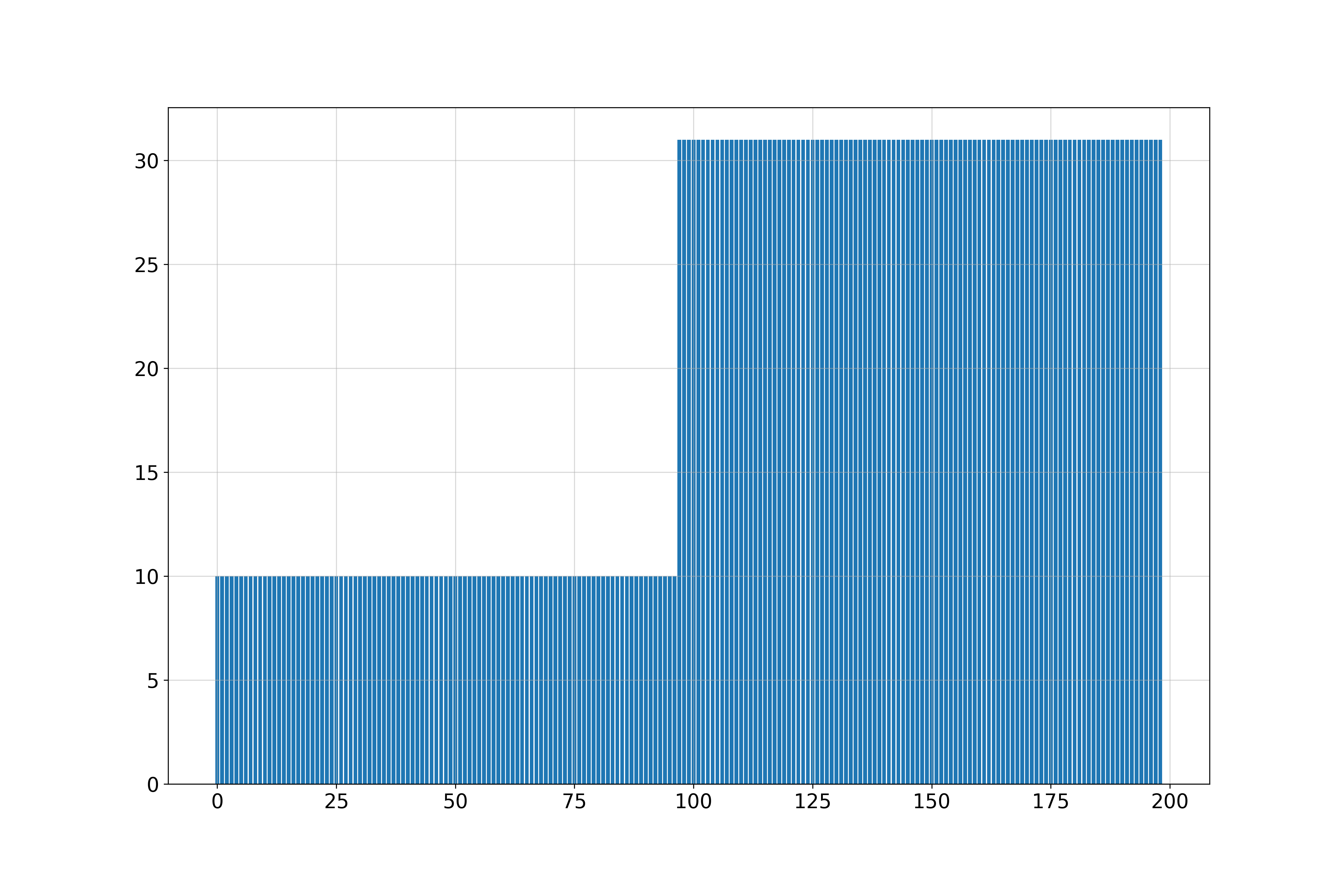
Union Dimensions

Image Manifolds

Square Manifold

Samples from the Square Manifold for different dimensions:

Square 10D
k=10
Square 20D
k=20
Square 100D
k=100

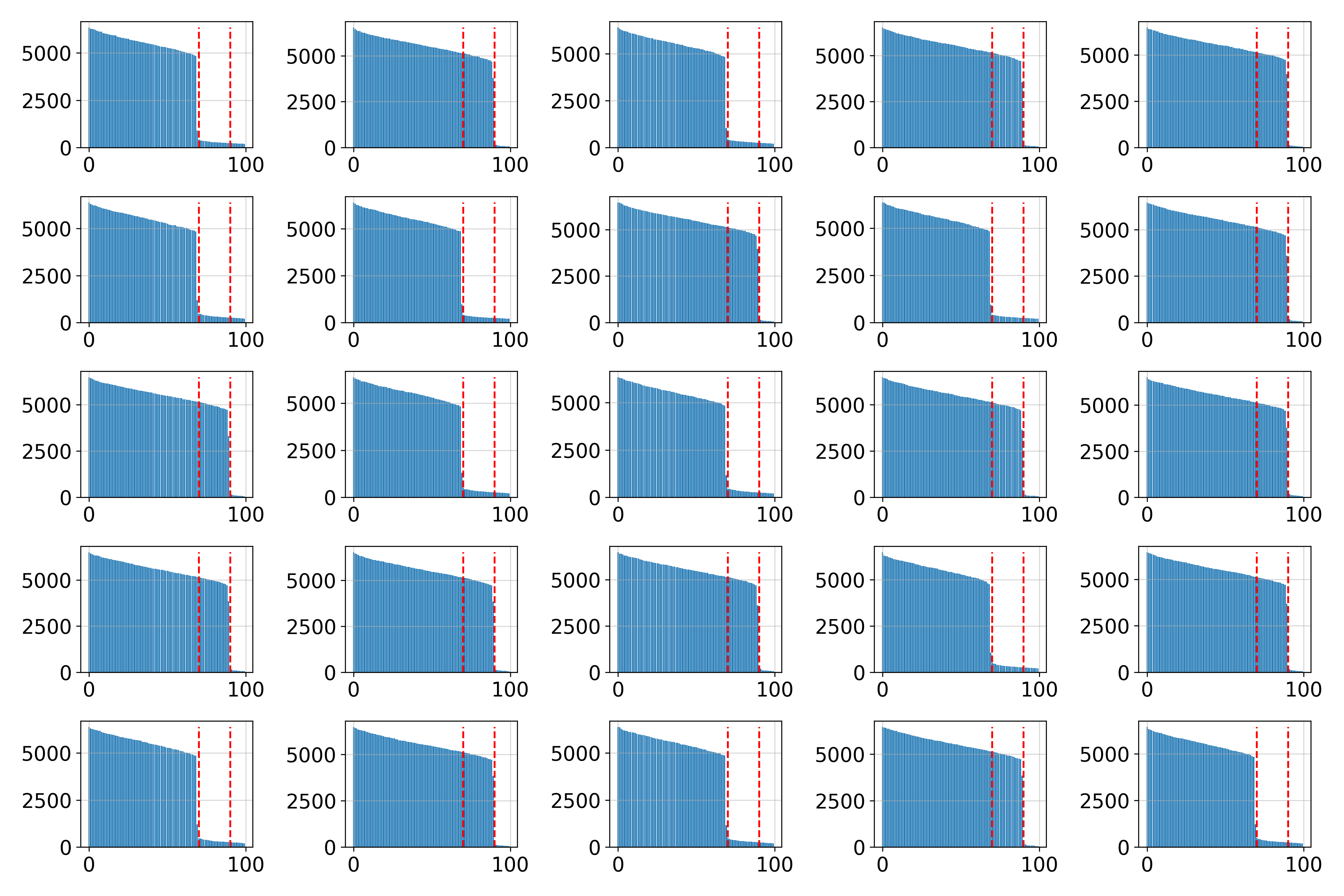
Spectra of singular values:

Square Spectrum Square Spectrum Adhoc

Gaussian Blobs Manifold

Samples from the Gaussian Blobs Manifold:

Gaussian 10D
k=10
Gaussian 20D
k=20
Gaussian 100D
k=100

Spectra of singular values:

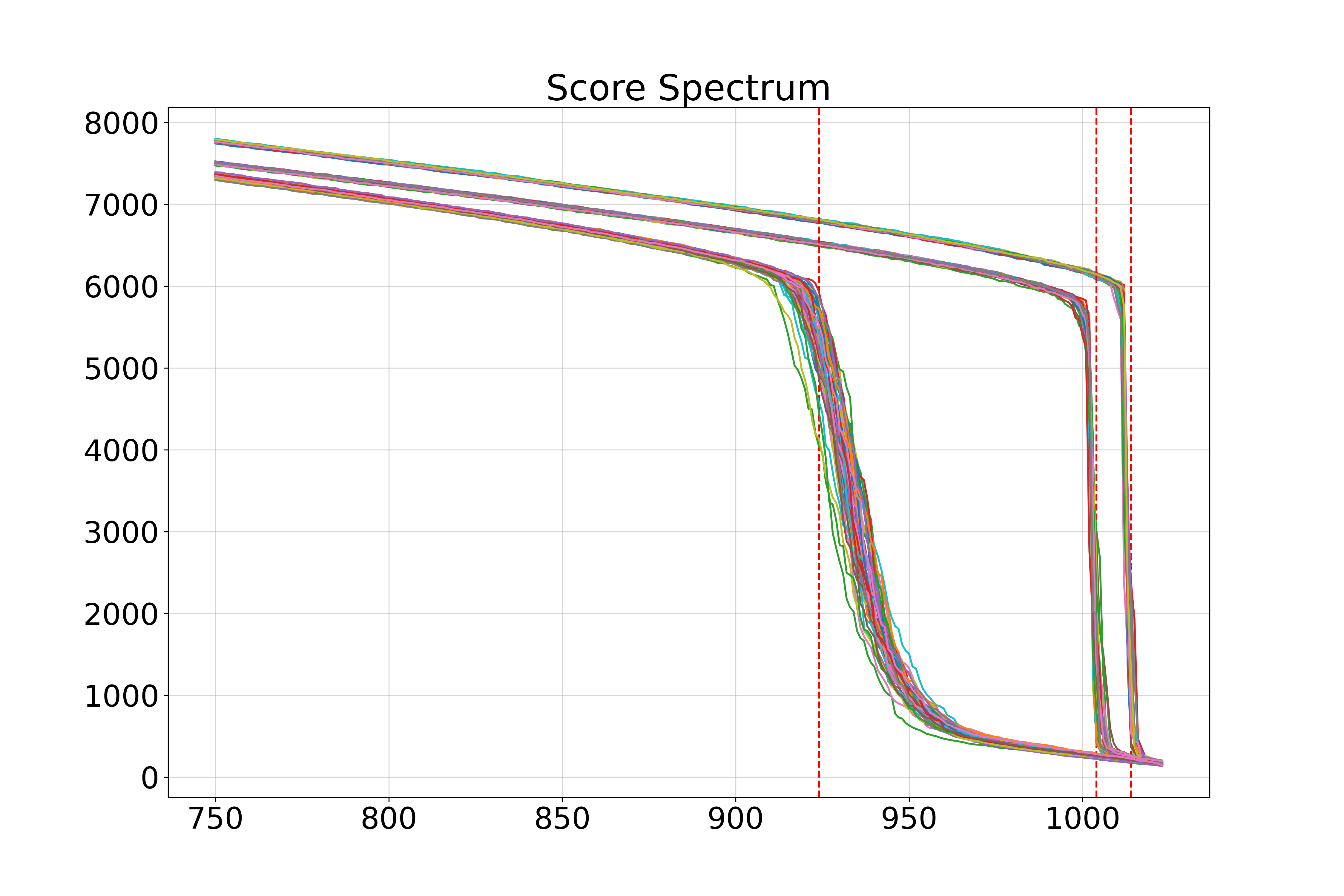
Gaussian Spectrum Gaussian Spectrum Adhoc

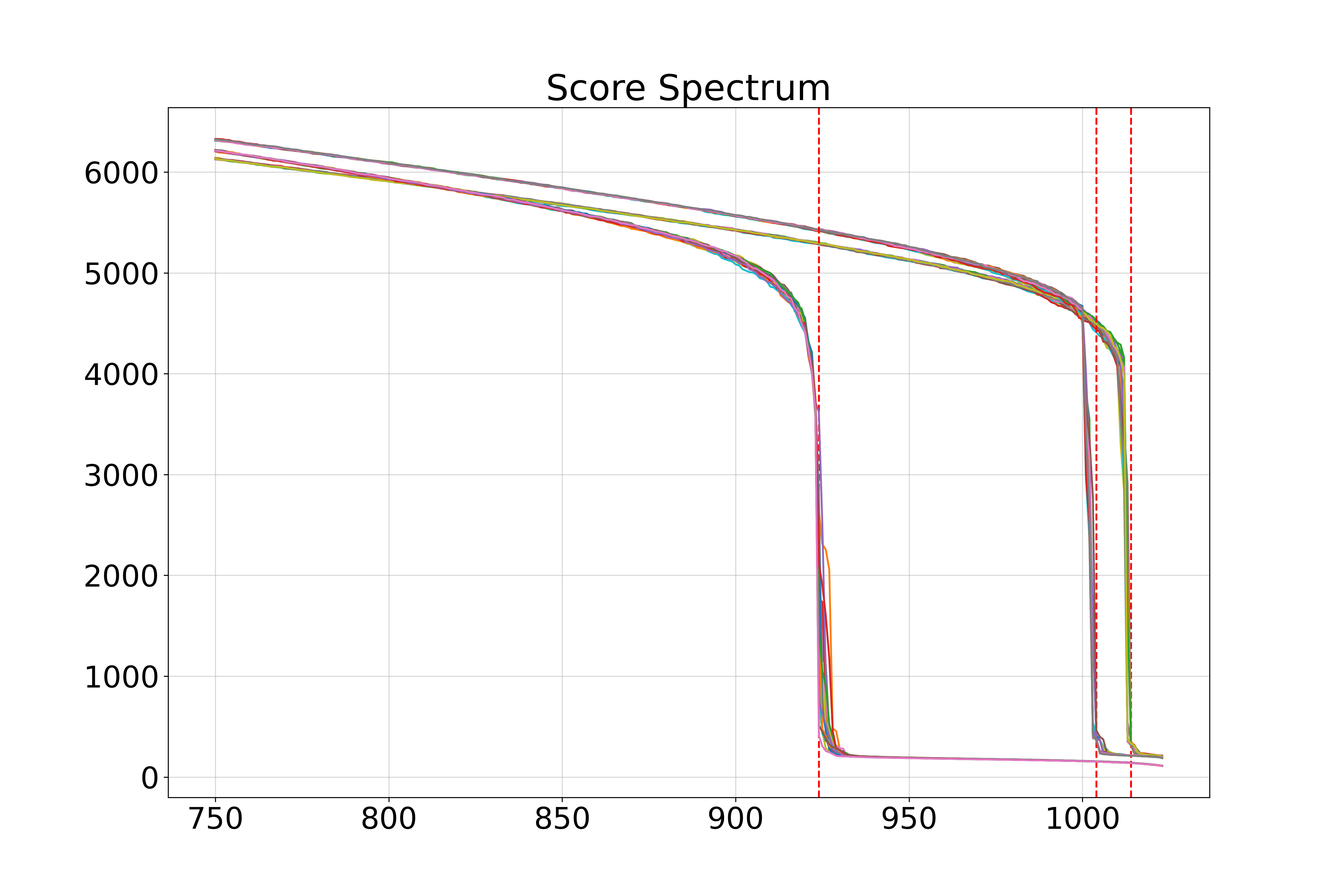
Real-World Data: MNIST

We applied our method to the MNIST handwritten digits dataset, analyzing each digit class separately.

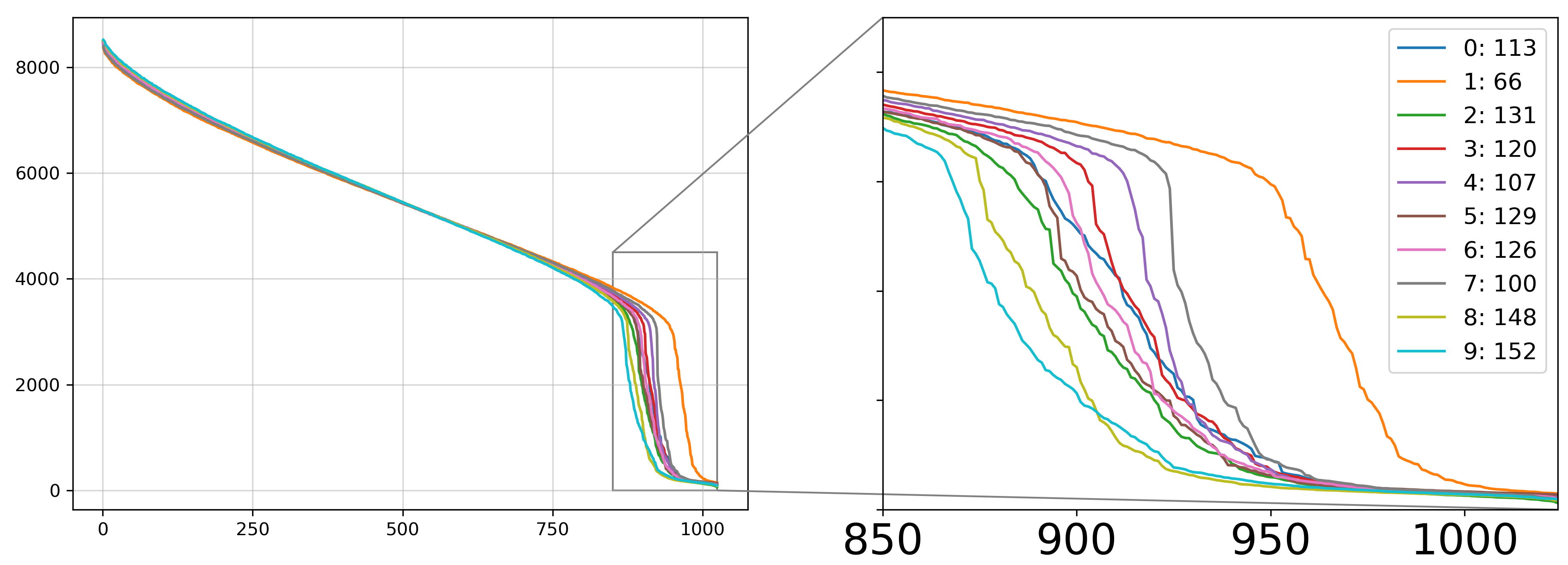
MNIST Score Spectra

Figure: MNIST Score Spectra

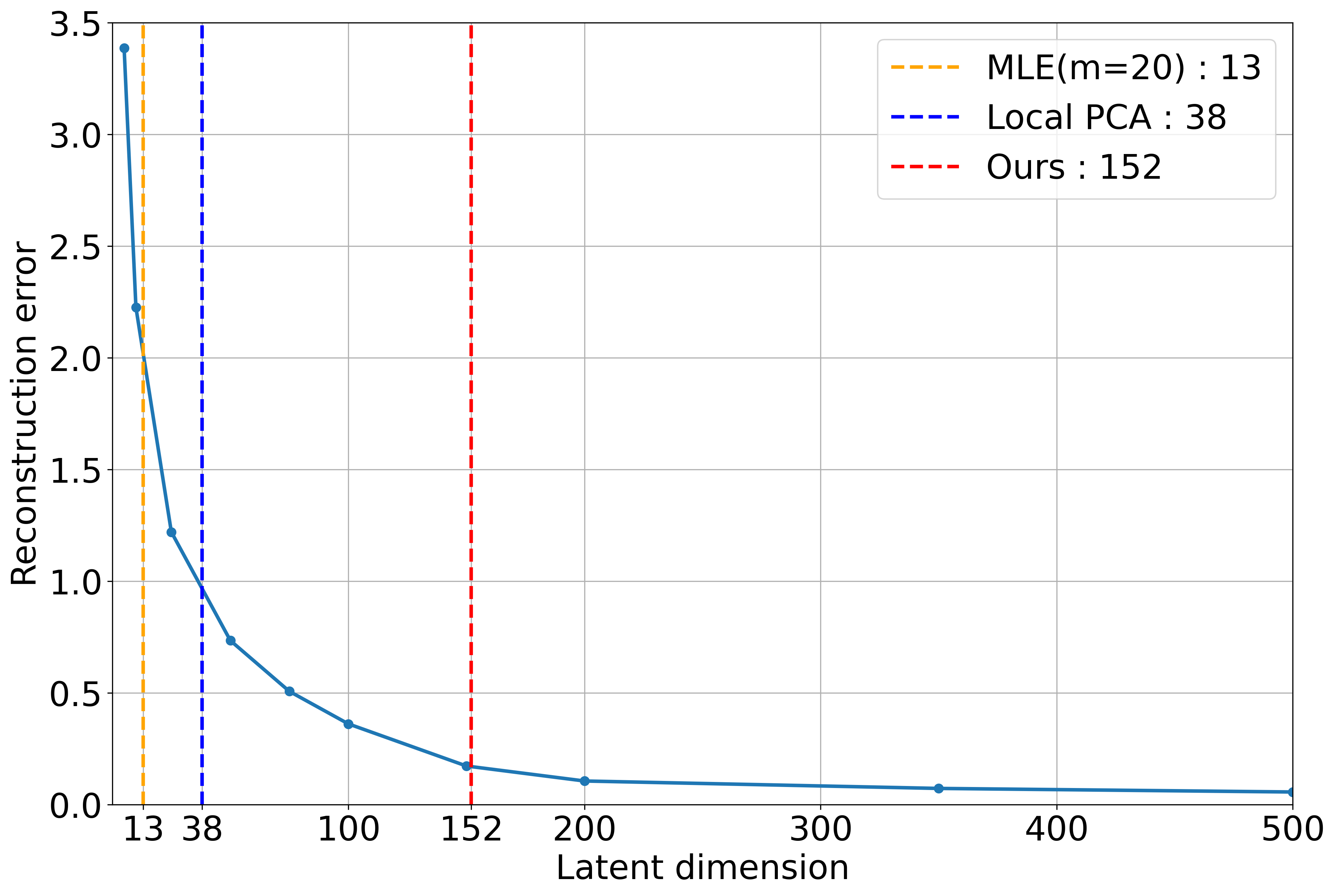
Autoencoder Validation

Figure: Autoencoder Validation

Estimated intrinsic dimensions for each digit:

Digit 0 1 2 3 4 5 6 7 8 9
Estimated \( \hat{k} \) 113 66 131 120 107 129 126 100 148 152

Summary of Experimental Results

We compared our method with other intrinsic dimension estimation techniques.

Dataset Ground Truth Ours MLE (m=5) MLE (m=20) Local PCA PPCA
Euclidean Data Manifolds
10-Sphere 10 11 9.61 9.46 11 11
50-Sphere 50 51 35.52 34.04 51 51
Spaghetti Line 1 1 1.01 1.00 32 98
Image Manifolds
Squares (k=10) 10 11 8.48 8.17 10 10
Squares (k=20) 20 22 14.96 14.36 20 20
Squares (k=100) 100 100 37.69 34.42 78 99
Gaussian Blobs (k=10) 10 12 8.88 8.67 10 136
Gaussian Blobs (k=20) 20 21 16.34 15.75 20 264
Gaussian Blobs (k=100) 100 98 39.66 35.31 18 985
MNIST
All Digits N/A 152 14.12 13.27 38 706

Limitations

  • Approximation Error: Caused by imperfect score approximation \( s_\theta(\mathbf{x}, t) \approx \nabla_{\mathbf{x}} \ln p_t(\mathbf{x}) \).
  • Geometric Error: Arises when \( t \) isn't sufficiently small, leading to:
    • Increased tangential components of the score vector.
    • Differences in normal spaces across sampled points due to manifold curvature.

Conclusions

  • Our estimator offers accurate intrinsic dimension estimates even for high-dimensional manifolds, indicating superior statistical efficiency compared to traditional methods.
  • This improvement is credited to the inductive biases of the neural network estimating the score function, the critical quantity for intrinsic dimension estimation.
  • Our theoretical results show that the diffusion model approximates the normal bundle of the manifold, providing more information than just the intrinsic dimension.
  • We can potentially use a trained diffusion model to extract other important properties of the data manifold, such as curvature.